两个向量的数量积为什么会是数量向量乘法计算公式介绍( 二 ) _知识分享

那么两个既有数量又带有方向的向量相乘，它们得到的结果，是不是也可以在不同的维度空间得到不同的解释呢？
答案是肯定的。
两个有方向的向量相乘，有两种方式：
1、两个向量可以是一维空间的向量（没有夹角），也可以是二维空间的向量（有夹角），它们相乘得到的结果既可以一维空间的数量关系，也可以得到从二维空间扩展到三维空间的带有方向的数量关系。
也就是说，两个带有方向的向量相乘的结果，也是有两个取向的：
一个是相乘后从二维空间坍缩为一维空间的数量，不再带有方向，就是我们中学课本的数量积的概念（称为“点乘”或者“内积”）。
此时，就必须放弃向量这个有向线段的方向，只是把有向线段的长度相乘：
如果两个向量同向，那它们本来都是一维空间，直接长度相乘就可以，不用坍缩。

文章插图
如果两个向量有夹角，那就把其中一个向量的长度和另一个向量在这个向量上的投影的长度相乘。

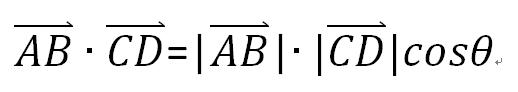
文章插图
如图：

文章插图
这样规定的目的只有一个：那就是我就要两个向量相乘之后在一维空间的数量关系而已，其它的我不管。
这就是数量积如此定义的目的所在。
这样强行规定的原因也很简单：第一、坍缩为一维空间之后，很多的数字运算规律在数量积的计算上依旧可用。
第二、这种坍缩符合物理标量的计算，能解决能量和矢量之间不可名状的转换问题。
比如力和位移相乘的结果就是一个不带有方向的能量。
第三、从纯粹数学的角度来说，能通过这种坍缩标定两个向量之间方向上的相似度。
如果是同向，那就是长度相乘；
如果有夹角，而且在锐角范围内，结果就比长度相乘的结果?。?
如果是直角，二者相乘结果为0，说明二者垂直，方向一点都不相似；
如果为负数，就说明二者方向方向夹角超过90度或者直接相反。
OK，说完了两个向量相乘结果的坍缩为数量关系的一个取向，我们接着说另外一个：
两向量相乘结果的另一种取向就和3*4扩展为二维空间的矩形面积一样，从平面向量的二维空间，扩展到三维立体空间（称之为“叉乘”或者“外积”）。
从这个意义上说，两个向量相乘的结果就是一个带有方向的量：
它的大小由这两个向量在二维平面围成的平行四边形面积确定，它的方向使用右手定则确定，垂直于这两个向量所在的二维平面。
也就是说，两个向量叉乘的结果是这两个向量决定的二维平面的法向量，它决定了一个在三维空间带有方向的量，这个新的向量的模是两个向量在二维平面构成的平行四边形的的面积。
由于向量叉乘的内容不在我们中学学习的范围之内，这里就不再多说。
总之，向量的数量积只是一个定义，因为课本没有解释它的来源，造成了学生的很多困惑，但愿本篇的这种解释，能对大家解除这种迷惑有所帮助。
更多的白话高中数学知识点的内容，大家可以参看我的合集《白话高中数学》
感谢您的阅读。

两个向量的数量积为什么会是数量 向量乘法计算公式介绍( 二 )

两个向量的数量积为什么会是数量向量乘法计算公式介绍( 二 )